이번 포스팅에서는 손으로 풀기 어려운 적분법을 컴퓨터로 이용한 방법으로 푸는 방법을 소개하겠다.
이는 패키지로도 잘 나와있지만 적분의 원초적인 개념을 안다면 패키지를 쓰는것에 그치지 않고 사용자의 입맛대로 적분을 구사 할 수 있게 된다.
수치해석적인 방법을 이용하여 적분을 진행하는데 있어 다음과 같이 진행됨을 미리 알린다.
1) 사다리꼴 적분방법
2) 사다리꼴 적분을 이용한 오차관계
3) R코드 실습
그리고 사전지식으로는 대학미적분학개념만 알고있으면 문제없다.
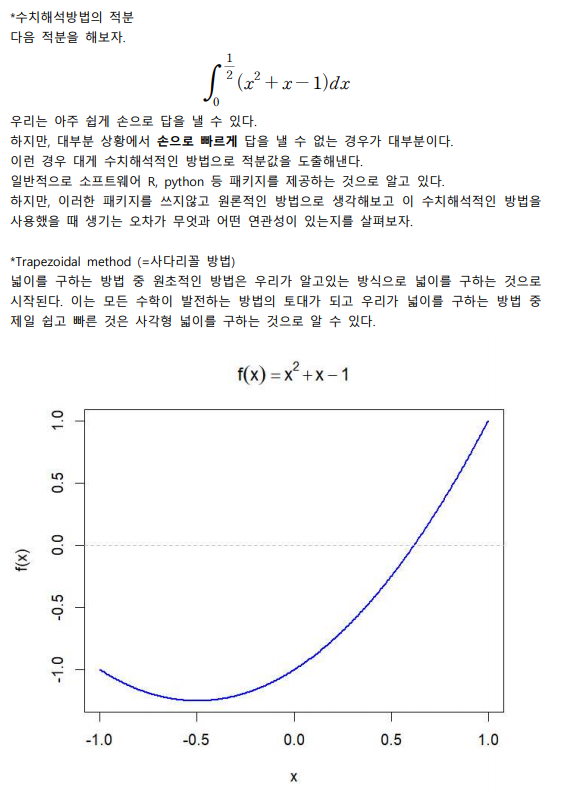
(1) 사다리꼴 적분방법

(2) 사다리꼴 적분을 이용한 오차관계



(3) R코드 실습
코드와 코드의 대한 설명을 부록해두었다.
#그래프 그리기
# 함수 정의
f <- function(x) x^2 + x - 1
# x의 범위 설정 및 그래프 그리기
x_vals <- seq(-1, 1, length.out = 400)
plot(x_vals, f(x_vals), type = "l", lwd = 2, col = "blue",
xlab = "x", ylab = "f(x)", main = expression(f(x)==x^2+x-1))
abline(h = 0, col = "gray", lty = 2) # x축 추가
# x = 0와 x = 1/2에서의 y값
x0 <- 0
x1 <- 0.5
y0 <- f(x0) # f(0) = -1
y1 <- f(x1) # f(1/2) = -0.25
# 사다리꼴의 꼭지점: (0, f(0)), (0.5, f(1/2)), (0.5, 0), (0, 0)
x_poly <- c(x0, x1, x1, x0)
y_poly <- c(y0, y1, 0, 0)
# 사다리꼴 그리기 (반투명)
polygon(x_poly, y_poly, col = rgb(1, 0, 0, 0.3), border = "red", lwd = 2)
# 점과 선 추가
points(c(x0, x1), c(y0, y1), col = "red", pch = 19)
segments(x0, y0, x1, y1, col = "red", lwd = 2)# 피적분 함수 정의
f <- function(x) {
return(x^2 + x - 1)
}
x <- seq(1,10,length.out = 5)
# 사다리꼴 법칙을 사용한 수치적분 함수
trapezoidal_int <- function(f, a, b, n) {
h <- (b - a) / n # 구간의 길이
x <- seq(a, b, length.out = n +1) # 구간을 n개의 점으로 나눔
y <- f(x) # 각 점에서의 함수값 계산
# 사다리꼴법 적용
int_value <- (h / 2) * (2 * sum(y) - y[1] - y[length(y)])
return(int_value)
}
# 적분 구간 [0,1]에서 적분 실행 (n을 증가시키면 정확도가 높아짐)
result <- trapezoidal_int(f, 0, 1/2, n = 2)
print(result)
origin <- -0.3333333
one_trape <- -0.3125
two_trape <- -0.328125
(origin-two_trape)/(origin-one_trape) #1/4 관계에 있음을 알 수 있다.


다음은 연습문제다.
코드로 푸는 문제, 손으로 푸는 문제와 미적분학의 개념에 대해서 묻는 문제이다.
답은 PDF파일로 올려두겠다.
1. f(x) = 1/x 을 [0,1]의 구간에서 위 적분법대로 적분하라.
2. f(x) = 1/x을 [-1,1]의 구간에서 위 적분법대로 적분하라.
3.Cauchy principal value에 대해서 설명해라.
4. f(x) =1/x을 [-1,1]의 구간에서 cauchy principal value을 구하라.
5. 문제 2번의 적분방법은 cauchy principal value인가?
6. f(x) = (1/sqrt(2*pi))*exp((x^2/2) )는 N(0,1)이다. 이때, 위 사다리꼴 적분법대로 [0,1/2]구간에서 적분하라. Fixed n =1000
7. f(x) = (1/sqrt(2*pi))*exp((x^2/2))는 N(0,1)이다. 이때, 위 사다리꼴 적분법대로 [0,1/2]구간에서 적분하라. Fixed n =2
8. f(x) = (1/sqrt(2*pi))*exp((x^2/2))는 N(0,1)이다. 이때, 위 사다리꼴 적분법대로 [0,1/2]구간에서 적분하라. Fixed n =3
9. 7번의 적분과 8번의 적분의 오차관계를 설명하라.
'미적분학' 카테고리의 다른 글
| 테일러 전개를 이용한 확장된 이항정리(음이항분포 MGF) (0) | 2024.08.21 |
|---|---|
| 테일러전개와 적용(라이프니츠적분정리) (2) | 2024.08.21 |
| 적분과 미분 순서를 바꿔도 되는 근거(라이프니츠 적분 정리) (0) | 2024.08.01 |
| 도함수를 배우는 이유(feat.미분계수) (0) | 2024.04.07 |
| 이차형식,Hessian Matrix를 이용한 다변수함수 판정법 (0) | 2024.04.06 |



