이번 포스팅은 일반기저를 직교기저로 변환시키는 방법에 대해서 소개하겠다.


우선 2차원으로 확인해보자.
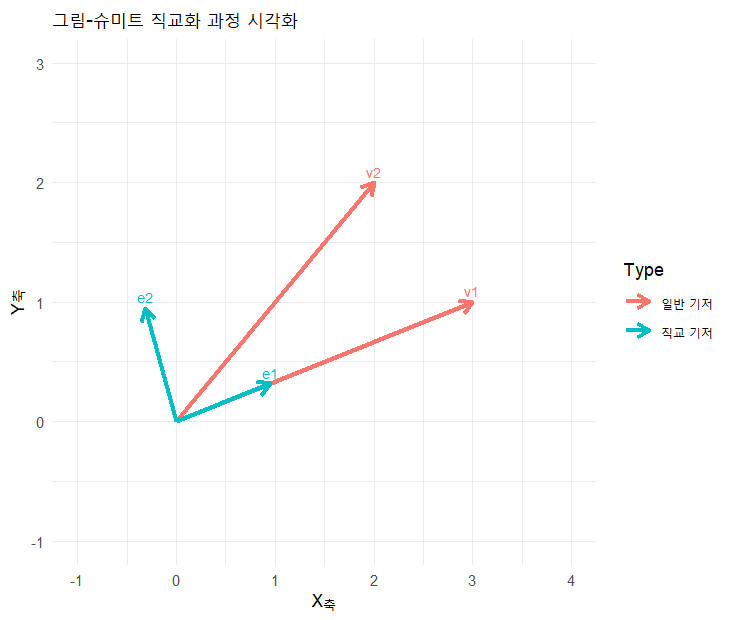
벡터가 직교가 됨을 한 눈에 볼 수 있다!
library(ggplot2)
library(grid)
# 직교기저가 아닌 벡터
v1 <- c(3, 1)
v2 <- c(2, 2)
# Gram-Schmidt 직교화 과정
# 첫 번째 직교 벡터는 그대로 v1
u1 <- v1
# 두 번째 벡터에서 u1의 성분 제거
proj_v2_on_u1 <- (sum(v2 * u1) / sum(u1 * u1)) * u1
u2 <- v2 - proj_v2_on_u1
# 정규화하여 직교 정규벡터(e1, e2) 생성
e1 <- u1 / sqrt(sum(u1 * u1))
e2 <- u2 / sqrt(sum(u2 * u2))
# 데이터 프레임으로 정리 (원점으로 시점벡터를 모으자!)
vectors <- data.frame(
xend = c(v1[1], v2[1], e1[1], e2[1]),
yend = c(v1[2], v2[2], e1[2], e2[2]),
Type = factor(c("일반 기저", "일반 기저", "직교 기저", "직교 기저"),
levels = c("일반 기저", "직교 기저"))
)
vectors$label <- c('v1','v2','e1','e2')
vectors
# ggplot2를 사용한 시각화
ggplot() +
geom_segment(data = vectors, aes(x = 0, y = 0, xend = xend, yend = yend, color = Type),
arrow = arrow(length = unit(0.3, "cm")), size = 1.2) +
xlim(-1, max(vectors$xend) + 1) +
ylim(-1, max(vectors$yend) + 1) +
labs(title = "그림-슈미트 직교화 과정 시각화",
x = "X축", y = "Y축") +
geom_text(data=vectors,
aes(x= xend,y=yend,label=label,color=Type),
vjust = -0.5,hjust=0.5,size=3,
show.legend = F)+
theme_minimal()
3차원은 어떨까?


library('rgl')
#----------------------------
# (1) 원래 벡터 3개 정의
#----------------------------
v1 <- c(3, 1, 2)
v2 <- c(2, 2, 1)
v3 <- c(1, 3, 2)
#----------------------------
# (2) Gram-Schmidt 직교화
#----------------------------
u1 <- v1
proj_v2_on_u1 <- (sum(v2*u1) / sum(u1*u1)) * u1
u2 <- v2 - proj_v2_on_u1
proj_v3_on_u1 <- (sum(v3*u1) / sum(u1*u1)) * u1
proj_v3_on_u2 <- (sum(v3*u2) / sum(u2*u2)) * u2
u3 <- v3 - proj_v3_on_u1 - proj_v3_on_u2
# 정규화 (단위 벡터)
e1 <- u1 / sqrt(sum(u1*u1))
e2 <- u2 / sqrt(sum(u2*u2))
e3 <- u3 / sqrt(sum(u3*u3))
#----------------------------
# (3) 원래 벡터 (빨간색) 시점을 원점으로 고정 후 시각화
#----------------------------
# v1
lines3d(rbind(c(0,0,0), v1), col = "red", lwd = 2)
points3d(v1, col = "red", size = 8)
text3d(v1*1.05 , texts = "v1", col = "red")
# v2
lines3d(rbind(c(0,0,0), v2), col = "red", lwd = 2)
points3d(v2, col = "red", size = 8)
text3d(v2*1.05 , texts = "v2", col = "red")
# v3
lines3d(rbind(c(0,0,0), v3), col = "red", lwd = 2)
points3d(v3, col = "red", size = 8)
text3d(v3 *1.05, texts = "v3", col = "red")
#----------------------------
# 직교 벡터 시점을 원점으로 고정
#----------------------------
# e1
lines3d(rbind(c(0,0,0), e1), col = "blue", lwd = 2)
points3d(e1, col = "blue", size = 8)
text3d(e1 * 1.1, texts = "e1", col = "blue")
# e2
lines3d(rbind(c(0,0,0), e2), col = "blue", lwd = 2)
points3d(e2, col = "blue", size = 8)
text3d(e2 * 1.1, texts = "e2", col = "blue")
# e3
lines3d(rbind(c(0,0,0), e3), col = "blue", lwd = 2)
points3d(e3, col = "blue", size = 8)
text3d(e3 * 1.1, texts = "e3", col = "blue")
#----------------------------
# (5) 축 및 시야각 설정
#----------------------------
axes3d()
title3d("Original Basis (Red) vs Orthonormal Basis (Blue)",
xlab = "X", ylab = "Y", zlab = "Z")
aspect3d("iso")
view3d(theta = 30, phi = 20, zoom = 0.9)'선형대수학' 카테고리의 다른 글
| LA21) 푸리에급수(Fourier series) (0) | 2025.03.21 |
|---|---|
| LA20)[R] 최적근사정리를 이용하여 근사해를 구하자 (0) | 2025.03.17 |
| LA18) 단위직교기저,직교기저를 활용한 선형결합 표현, 벡터 정사영 (0) | 2025.03.14 |
| LA17) 직교(orthogonal),직교여공간(orthogonal complement) (0) | 2025.03.14 |
| LA16) 내적(inner product),내적공간 (0) | 2025.03.14 |



