[R] harmonic regression을 이용한 서울시 초미세먼지 예측

1. harmoic reg(조화 회귀)이란?

https://pastryofjsmath.tistory.com/91

[R] AirPassengers 데이터를 이용한 회귀분석 비교(회귀분석,동적회귀)

2. 푸리에급수란?

https://pastryofjsmath.tistory.com/92

LA21) 푸리에급수(Fourier series)-1

 

3.  데이터

공공데이터 포털에서 서울시 미세먼지에 대한 데이터를 가져옴.

미세먼지에 영향이 있는 여러 요인들을 더 탐색해서  하고 싶었으나 시간상 여유가 안되어서 이렇게 진행함.

https://www.data.go.kr/data/15089266/fileData.do

서울특별시_시간별 (초)미세먼지_20221231

 

4.  데이터 전처리,시각화

rm(list=ls())
gc()
data <- read.csv('C:/Users/PJS/Desktop/R 데이터/서울특별시_시간별 (초)미세먼지_20221231/서울시 대기질 자료 제공_2008-2011.csv',header = T,fileEncoding = 'CP949')
#library(dplyr)
#data %>% View()
data$구분 <- as.factor(data$구분)
data %>% View()
#library(ggplot2)
#ggplot은 필터링된 데이터를 직접 참조가 안됨.


#필터링은 둘 다 가능함 원하는 방식대로 사용
new_data <-data[(data$구분 %in% c('관악구','강동구','강남구','강서구','강북구')),]
new_data <- data %>% filter(구분 %in% c('관악구','강동구','강남구','강서구','강북구'))


#levels(new_data$구분)
#unique(new_data$구분)
#결측 데이터 체크
colSums(is.na(new_data))
na.omit(new_data)
rownames(new_data) <- 1:nrow(new_data)

 

데이터 수가 10만개가 넘어갑니다. 시간별 데이터로 되어있기에 일별,월별 등으로 전처리 과정이 필요합니다.

여기서는 group_by()를 이용하여 일별 데이터로 전처리 했습니다.

 

여기서 날짜 데이터 전처리 방법을 잘 모르시는분은 

https://pastryofjsmath.tistory.com/35

날짜 데이터 전처리 [in R] -strptime,str_extract(),substr()

 

new_data$일시 <- strptime(x = new_data$일시,format= '%Y-%m-%d%H:%M')

new_data$날짜 <- as.Date(new_data$일시)


daily_summary_mean_pm25 <- new_data %>% group_by(날짜,구분) %>% summarise(평균_PM25 = mean(초미세먼지.PM25.,na.rm = T)) %>% ungroup()
daily_summary_mean_pm25
daily_summary_mean_pm25<-na.omit(daily_summary_mean_pm25)

str(daily_summary_mean_pm25)


> str(daily_summary_mean_pm25)
tibble [7,053 × 3] (S3: tbl_df/tbl/data.frame)
 $ 날짜     : Date[1:7053], format: "2008-01-01" "2008-01-01" "2008-01-01" ...
 $ 구분     : Factor w/ 26 levels "강남구","강동구",..: 2 3 4 5 2 3 4 5 2 3 ...
 $ 평균_PM25: num [1:7053] 15.6 13.1 13.1 12 18.5 ...
 - attr(*, "na.action")= 'omit' Named int [1:87] 233 238 279 284 3302 3307 3312 3368 3373 4568 ...
  ..- attr(*, "names")= chr [1:87] "233" "238" "279" "284" ...
  
  ggplot(data=daily_summary_mean_pm25, aes(x = 날짜, y= 평균_PM25,color=구분))+
  geom_line()+
  theme_minimal()+
  labs(title = "구별 일별 초미세먼지(PM2.5) 추이",
       x = "날짜", y = "평균 PM2.5 (㎍/㎥)")+
  ylim(0,200)


ggplot(daily_summary_mean_pm25, aes(x = 날짜, y = 평균_PM25)) +
  geom_line(color = "steelblue") +
  facet_wrap(~ 구분, ncol = 2) +
  labs(title = "구별 일별 초미세먼지(PM2.5) 추이 (facet)",
       x = "날짜", y = "평균 PM2.5 (㎍/㎥)") +
  theme_minimal()+
  ylim(0,200)

상당히 어지럽고 그래프의 추세선도 잘 보이지 않습니다. 그럴때는 다음과 같이 요인별로 분류하면 됩니다.

여기서 "관악구"를 예측해보겠습니다.

gwanakgu <- daily_summary_mean_pm25 %>% filter(구분 == '관악구')
N<- nrow(gwanakgu)
t <- 1:N
logy <- log(gwanakgu$평균_PM25)
gwanakgu$평균_PM25 <- logy

train_idx <- 1:round(0.7*N)
test_idx <- (round(0.7*N)+1) : N

train_df <- gwanakgu[train_idx,]
test_df <- gwanakgu[test_idx,]

t_train <- 1:nrow(train_df)
t_test <- (nrow(train_df)+1):(nrow(train_df)+nrow(test_df))

create_fourier_feat <- function(time,K,period){
  cos_terms <- sapply(1:K, FUN = function(k) cos(2*pi*k*time/period))
  sin_terms <- sapply(1:K, FUN = function(k) sin(2*pi*k*time/period))
  
  fourier_feat <- cbind(cos_terms,sin_terms)
  colnames(fourier_feat) <- c(paste0('cos',1:K),paste0('sin',1:K))
  return(fourier_feat)
}

반드시! 순서대로 t를 지정해주셔야 합니다. 시계열로 보겠다는 것이니까요.

#훈련데이터 fitting
fourier_train <- create_fourier_feat(t_train,K=3,period=7)
fourier_train_df <- cbind(y=train_df$평균_PM25,fourier_train)


fourier_test <- create_fourier_feat(t_test,K=3,period=7)


model_fourier <- lm(y~.,data=data.frame(fourier_train_df))
pred_log <- predict(model_fourier, newdata= as.data.frame(fourier_test))
pred <- exp(pred_log)
actual_y  <- exp(test_df$평균_PM25)
mse_fourier <- mean((actual_y - pred)^2,na.rm = T)
mse_fourier
[1] 294.1781

# SSR: 예측값과 평균값 사이의 제곱합
ssr <- sum((pred - mean(actual_y))^2)
# SST: 실제값과 평균값 사이의 제곱합
sst <- sum((actual_y - mean(actual_y))^2)
# 테스트셋 기준 R²
r2_test <- ssr / sst
cat("테스트셋 기준 R²:", round(r2_test, 4), "\n")
테스트셋 기준 R²: 0.0377

df<-data.frame(pred=pred,y=exp(test_df$평균_PM25))

plot(gwanakgu$날짜,exp(gwanakgu$평균_PM25),type='l',ylim=c(0,50))
lines(test_df$날짜,pred,col='blue',lwd=1,lty=2)
legend("topleft", legend = c("실제값", "Fourier 회귀 예측"),
       col = c("grey", "blue"), lty = c(1,2), lwd = 2)

처참한 수준입니다..

하지만 파라미터 k를 조절해서 더 타이트하게 만들 수 있습니다.

 

gwanakgu$log_PM25 <- log(gwanakgu$평균_PM25)

train_df <- gwanakgu[train_idx, ]
test_df  <- gwanakgu[test_idx, ]

t_train <- 1:nrow(train_df)
t_test  <- (nrow(train_df)+1):(nrow(train_df)+nrow(test_df))

#period와 K 조정
K <- 1200
period <- 7

fourier_train <- create_fourier_feat(t_train, K = K, period = period)
fourier_test  <- create_fourier_feat(t_test,  K = K, period = period)

model_fourier <- lm(log_PM25 ~ ., data = data.frame(log_PM25 = train_df$log_PM25, fourier_train))

pred_log <- predict(model_fourier, newdata = as.data.frame(fourier_test))
pred <- exp(pred_log)
actual_y <- test_df$평균_PM25

mean((actual_y - pred)^2,na.rm=T)


# 시각화
plot(gwanakgu$날짜, exp(gwanakgu$평균_PM25), type='l')
lines(test_df$날짜, exp(actual_y), col='blue', lwd=1, lty=2)
legend("topleft", legend = c("실제값", "Fourier 회귀 예측"),
       col = c("grey", "blue"), lty = c(1,2), lwd = 2)

# SSR: 예측값과 평균값 사이의 제곱합
ssr <- sum((pred - mean(actual_y))^2)

# SST: 실제값과 평균값 사이의 제곱합
sst <- sum((actual_y - mean(actual_y))^2)

# 테스트셋 기준 R²
r2_test <- ssr / sst
cat("테스트셋 기준 R²:", round(r2_test, 4), "\n")

얼핏보기엔 잘 예측된다. 라고 볼 수 있지만 

이것에 대한 설명력은 어떻게 될지는 아직 모릅니다. 

K값을 늘려가면서 R2가 어떻게 변화하는지 시각적으로 보는 코드입니다.

오래걸리고 메모리를 많이 먹기에 주기적으로 아래 코드로 메모리를 비워주세요.

rm(list=ls())
gc()

 

for (i in seq_along(K_vals)) {
  K <- K_vals[i]
  ft_train <- create_fourier_feat(t_train, K, period = 7)
  ft_test  <- create_fourier_feat(t_test,  K, period = 7)
  
  model <- lm(log_PM25 ~ ., data = data.frame(log_PM25 = train_df$log_PM25, ft_train))
  pred_log <- predict(model, newdata = as.data.frame(ft_test))
  pred <- exp(pred_log)
  
  ssr <- sum((pred - mean(actual_y))^2)
  sst <- sum((actual_y - mean(actual_y))^2)
  results$R2_test[i] <- ssr / sst
}

plot(results$K, results$R2_test, type = 'b',
     main = "K에 따른 테스트셋 R² 변화",
     xlab = "K", ylab = "R² (Test)")

저는 중간에 멈추었기에 1500까지만 그려졌습니다. 

하지만 파라미터를 계속 키워서 확 과적합시켜버리면 의미가 없을테니까

하나의 지표 MSE를 R2와 비교해가면서 확인하면 될 것 같습니다.

K_vals <- seq(1200, 1500, by = 50)

results <- data.frame(K = K_vals, R2_test = NA, MSE_test = NA)

for (i in seq_along(K_vals)) {
  K <- K_vals[i]
  
  # Fourier 특성 생성
  ft_train <- create_fourier_feat(t_train, K, period = 7)
  ft_test  <- create_fourier_feat(t_test,  K, period = 7)
  
  # 모델 학습
  model <- lm(log_PM25 ~ ., data = data.frame(log_PM25 = train_df$log_PM25, ft_train))
  pred_log <- predict(model, newdata = as.data.frame(ft_test))
  pred <- exp(pred_log)
  
  # 성능 지표 계산
  actual_y <- test_df$평균_PM25
  ssr <- sum((pred - mean(actual_y))^2, na.rm = TRUE)
  sst <- sum((actual_y - mean(actual_y))^2, na.rm = TRUE)
  r2_test <- ssr / sst
  mse_test <- mean((actual_y - pred)^2, na.rm = TRUE)
  
  results$R2_test[i] <- r2_test
  results$MSE_test[i] <- mse_test
}

#R² & MSE 동시 시각화
plot(results$K, results$R2_test, type = 'b', col = "blue", lwd = 2,
     xlab = "K", ylab = "R² (파랑) / MSE (빨강)",
     main = "K 값에 따른 테스트셋 R²와 MSE 변화")

# 두 번째 y축: par(new=TRUE)
par(new = TRUE)

plot(results$K, results$MSE_test, type = 'b', col = "red", lwd = 2, axes = FALSE,
     xlab = "", ylab = "")
axis(side = 4, col = "red", col.axis = "red")
mtext("MSE (빨강)", side = 4, line = 3, col = "red")

legend("bottomright", legend = c("R² (Test)", "MSE (Test)"),
       col = c("blue", "red"), lty = 1, lwd = 2)

 

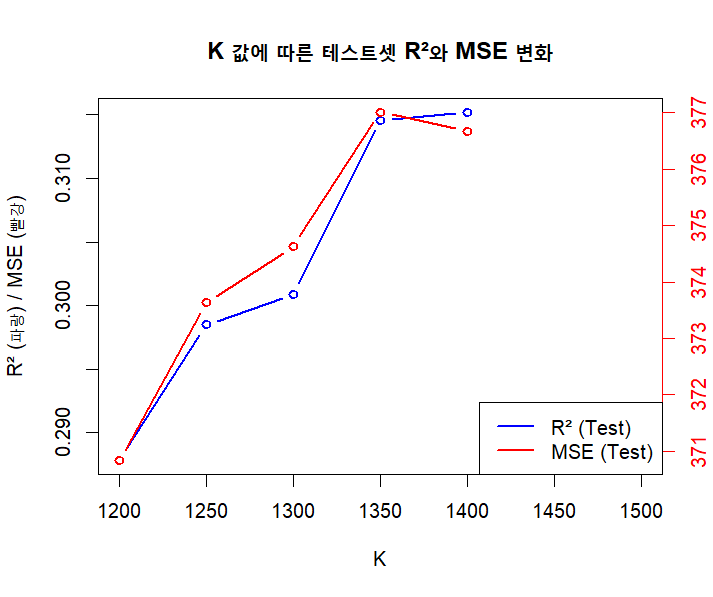
서로 값이 겹치는 구간이 존재하는데 저기 값을 파라미터로 쓰면 되겠습니다.

 

 

전체코드는 아래 깃허브에 올려두었습니다.

https://github.com/juseong4121/R

GitHub - juseong4121/R