대수의 법칙과 중심극한의 정리

중심극한정리가 뭔지 아냐고 물어본적이 있다. 그래서 정규분포로 수렴하는게 아닌가요?라고 답한적이 있는데, 실은  뭐가 정규분포로 수렴하는지에 대해 더 정확하게 서술해야한다.그래서 바로 중심극한정리(CLT)를 소개하고 싶었는데, 이는 대수의 법칙부터 연결되어 있어서 모두 소개하기로 한다. 

내용은 수리통계학을 근간으로 했다.

 

대수의 법칙

 

Th 3.12

이를 이해하는데 있어, 첫 번째로 알아야 할 내용이 마르코프 확률부등식(Markov Ineq.)이다. 이는 이후의 체비셰프 확률부등식을 이해하는데 있어 키포인트가 된다.

아래는 마르코프 확률부등식 증명과정이다. 

아래 마르코프 확률부등식을 요약하자면,

어떤 실함수가 경계보다 작을 확률은 '기댓값/경계값'보다 항상 작거나 같다는 의미이다.

마르코프 확률부등식 증명-1

 

마르코프 확률부등식 증명-2

 

 

 

쳬비셰프 부등식은 이렇게 기억하면 편하다.

'분포의 디폴트 하한값 제공'

쳬비셰프 확률부등식 1

체비셰프 확률부등식 -2

체비셰프의 성질

체비셰프가 뭐길래 그렇게 중요하다 할까?

체비셰프는 분포의 특성을 몰라도 가장 기본적인 하한값을 정해준다. 아무 특성을 모르지만 경계치를 정해준다니..

매우매우 중요하다고 할 수 있다. 

우리의 목표는 Thm3.12 표본평균이 모평균으로 확률적수렴하는 것을 증명하려고 이 긴 내용을 보는 것이다.

아래는 코시-슈바르츠 부등식이다.

통계에서의 코시-슈바르츠 부등식

코시-슈바르츠 부등식 증명-1

코시-슈바르츠 부등식 증명-2

 

코시-슈바르츠 부등식 증명-3

코시-슈바르츠 부등식 증명-4

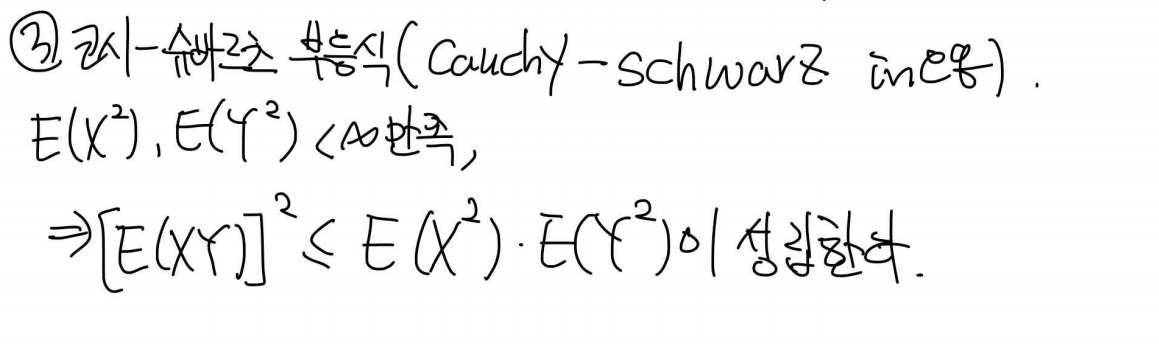
이제 거의 다왔다. 이제 더 큰 틀인 분포수렴에 대해서 알아보자.

분포수렴 정의

이는 분포자체도 수렴성이 있다는 "정의"를 의미한다. 집요하게 의문을 가지지 말자.