[R] ch4-2) 다변량 조건부 정규분포 평균,공분산 유도,코드구현

증명 테크닉에서 다변량 정규분포  mgf를 유도하는 과정이 비슷하게 담겨있습니다.  내용은 수리통계학에서 배우지만 여기 카테고리에 담겠습니다.

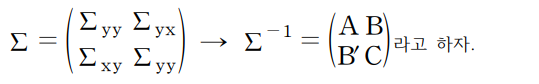
여기서 R은 잔여항 즉, 우리가 흔히 2차함수을 완전제곱꼴로 만들면 나오는 상수항입니다. 밑에 풀이과정있습니다. 잔여항은 특성구하는데 중요한 역할을 하지 않으므로 구하지 않습니다.

아래 예제 문제입니다.

rencher : linear model in statistics

아래는 이에 대한 해설이고 이를 코드로 구현하는 과정을 서술하려고 합니다.

사용자지정 함수를 만들어서 일반화하는 방식과 이에 대한 패키지를 쓰는 것 모두 보여드리겠습니다.

# 전체 평균 벡터
mu <- c(2, 5, -2,1)
Sigma <- matrix(c(9,0,3,3,
                  0,1,-1,2,
                  3,-1,6,-3,
                  3,2,-3,7), nrow=4, byrow=TRUE)

# y1,y2 | y3, y4 를 구해야 하므로
index <- c(1,2,3,4) 
# y1,y3 |y2, y4 -> (1,3,2,4)로 새롭게 인덱싱.
#하지만 우리는 1,2,3,4 그대로 쓰면됨.
target_index <- index[1:2]
given_index <- index[3:4]

Sigma_index <- Sigma[index, index]

# 분리
mu1 <- mu[target_index]                  # (y1,y2) 평균
mu2 <- mu[given_index]                # (y3, y4) 평균
Sigma11 <- Sigma[target_index, target_index]         # cov(y1,y2)
Sigma12 <- Sigma_index[target_index, given_index]       # cov((y1,y2), (y3, y4))
Sigma22 <- Sigma_index[given_index, given_index]    # cov((y3, y4))

# 관측값 예시: y3 = a, y4 = b
a <- 1     # 예시값 (y3)
b <- 0     # 예시값 (y4)
x <- c(a, b)

# 조건부 평균 계산
cond_mean <- mu1 + Sigma12 %*% solve(Sigma22) %*% (x - mu2)
cond_mean == c(3+ 10/11 , 14/3 - 1/33)




#####함수이용####
get_conditional_mean <- function(mu, Sigma, target_index, given_indices, x_given) {
    mu1 <- mu[target_index]
    mu2 <- mu[given_indices]
    Sigma11 <- Sigma[target_index, target_index]
    Sigma12 <- Sigma[target_index, given_indices]
    Sigma22 <- Sigma[given_indices, given_indices]
    cond_mean <- mu1 + Sigma12 %*% solve(Sigma22) %*% (x_given - mu2)
    return(cond_mean)
}

mu <- c(2, 5, -2,1)
Sigma <- matrix(c(9,0,3,3,
                  0,1,-1,2,
                  3,-1,6,-3,
                  3,2,-3,7), nrow=4, byrow=TRUE)


get_conditional_mean(mu, Sigma, target_index = c(1,2), given_indices = c(3,4), x_given = c(1,0))





#####package####
# y2 | (y1, y3)의 조건부 평균과 공분산 구하기
# 조건부 분포: y = (y1, y2, y3)에서
# -> 조건: y1 = 2, y3 = 3
# -> target index = 2, given = c(1,3)

# mean and covariance
cond <- condMVNorm::condMVN(mean = mu,
                            sigma = Sigma,
                            dependent.ind = 2,        # y2
                            given.ind = c(1,3),        # y1, y3
                            X.given = c(2,3))          # 값 대입

cond$condMean      # 조건부 평균
cond$condVar       # 조건부 분산